This guest blog post was written by Layne Price.
I’ll let you in on a little secret about inflation: we don’t know really know any of the details. This might or might not be surprising to you, but it’s not often advertised — although it does keep us working hard!
Let’s start with what we do have: a nice and simple understanding of a basic inflationary mechanism, which has lots of successes — namely, flattening, smoothing, but ever-so-slightly wrinkling our universe. These are things that we do observe and that most people agree we don’t have a satisfactory description for, outside of invoking inflation.
So, what’s the problem?
This simple understanding falls well short of what is actually going on. Inflation happens during a complex era of the universe’s history, which has energies that vastly exceed anything we will likely ever be able to test in a laboratory. Importantly, we do not have an experimentally confirmed theory that we can study for clues at this energy scale, since physics’ workhorse, the Standard Model, breaks down spectacularly.
Consequently, the inflationary models we use are by-and-large “toy” descriptions of something realistic, but beyond our current reach. What I mean by this is that we try to pare down a complicated theory by ignoring possible features it might contain until we are left with only the bare essence of what we need in order to get inflation. We then study this overly simplistic toy model because it’s easier and captures the most important details.
Unfortunately, while this is simple (and Ockham would certainly approve), these toy models have been found lacking. The most obvious problem is that the simplest of all possible models — inflation driven by one single massive field — is under very serious pressure from the Planck satellite, since it predicts more gravitational waves than we can reconcile with the observations of the cosmic microwave background (CMB).
So, if the simplest models don’t work, what are we supposed to do? Let’s say we want to cook up a better inflation model. To start with, we first want to find some sort of exotic material to drive inflation, but there’s nothing obvious in the standard theories. OK, then — what non-standard ingredients do we have? A typical roll-call from high energy theories goes something like this: supergravity; Type I, Type IIa, Type IIb, and heterotic string theories; modified gravity; compactifications of extra dimensions into a high-dimensional landscape; a buffet of supersymmetric extensions to the Standard Model; axions, instantons, galileons — and this just scratches the surface. It’s confusing and unlikely that we will all come to an agreement about exactly which ingredients are right.
However, what each of these theories gives us is the freedom to add lots of new knobs and dials we can play with to tease out a combination of parameters that gives us something sensible. With a complicated enough machine hooked up to the toy models, it’s not so surprising that we can tune it to find lots of interesting things that match the data very well.
The toy picture of inflation has only a few dials we can turn. However, if we hook it up to the high energy Franken-machine, there are almost endless possibilities.
So, now we ask ourselves, “Do we find this approach convincing?” If we were to include everything in the fridge in our recipe, weigh all our ingredients precisely, cook the theory just right, and get a great new scenario, would you believe it? We may be very fond of the exact combination of knobs and dials we tuned to predict the data, but of course there is nothing to guarantee that this is what actually happened in the real Universe – many different settings could have led to the same outcome!
Luckily there’s something we can do so that we don’t have to have a complete understanding of the high energy theory. Suppose we have an inflation model with one parameter X, and we need X to get a prediction, which we’ll call Y, from the model. Inflationary parameters might be things like a quantum field’s mass or initial conditions; and, as we discussed above, realistic models have many parameters. But, we’ll use X as a placeholder in a general model.
It’s common that we don’t know what the exact value of X is. High energy theory is notoriously hard, after all. So, it’s typical to quit and leave the problem here, since we’re now stuck: we don’t know X, and Y depends on X, so we need more info. However, we do have some extra information floating around somewhere; we just need to gather it.
Let’s collect what we do know in this hypothetical example:
- Well, I suppose X should be positive and that X=10,000 is unrealistically high, for whatever reason.
- However, X=1, X=10, X=100, and X=1,000 all seem like they are perfectly reasonable values.
- If X=1, then I can calculate Y=1; if X=10, then Y=2; if X=100, Y=3; etc.
We will use this information by first drawing an analogy between “uncertainty in X” and “a random variable X.” Because we are uncertain about the exact value of parameter X, we can instead randomly set the dial that tunes this parameter according to our beliefs outlined above. We calculate the prediction Y and think of this as one of many possible values Y could have. We then repeat the process many times to build a large sample of the model’s prediction. Instead of having one simple prediction, the model then has a range of possible predictions that are weighted according to this random sample. The hope is that a good model will have a small spread for its predictions.
In our recent paper we took this a step further and used the power of the Central Limit Theorem to give us easily characterized results for the CMB, in terms of far fewer parameters than you might naively expect. The Central Limit Theorem says that independent random variables (our model’s parameters) act like a single normally distributed variable when you add a bunch of them together. A normal distribution has only two parameters, the mean and variance, which effectively cancels out a lot of the model’s complexity, leaving only a few dials that we can tune in our inflationary machinery.
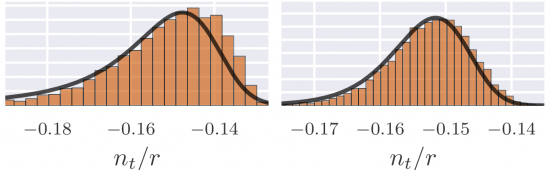
A prediction for the CMB, with a different number of degrees of freedom in the underlying model. The inflationary consistency relation, measured by the ratio n/r fits very closely to what is predicted by the Central Limit Theorem.
We did this for one of the most interesting observables, which is called the “inflationary consistency relation,” which relates the gravitational waves produced during inflation to the wrinkles in the universe’s curvature. In principle, we can measure this using the hot and cold spots in the CMB or by galaxy surveys. The “toy” inflation models all predict the exact same thing, while the more realistic models with many degrees of freedom can break it. However, we were able to show that a large class of the complicated models actually give a sharp prediction, which becomes more and more precise as we add more complexity to the model (in terms of numbers of quantum fields). This is more evidence that models with lots of knobs and dials can be surprisingly insensitive to their exact settings. Hopefully this means that we only have to know the broad-strokes of the high energy theories in order to get simple answers, similar to our well-studied toy models.
So, I suppose the moral of the story is: even a complicated recipe should still give us a simple cake in the end, and you can tell a simple recipe and a complex recipe apart by looking at the cake!
You can read more here:
L.C. Price, H.V. Peiris, J. Frazer, R. Easther
Gravitational wave consistency relations for multifield inflation
R. Easther, J. Frazer, H.V. Peiris, L.C. Price
Simple predictions from multifield inflationary models
