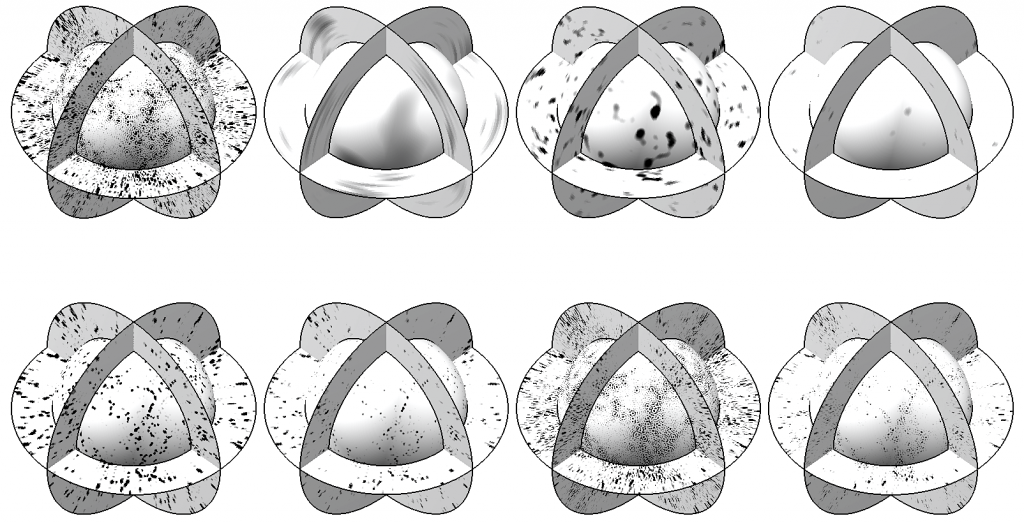
Last May, Boris Leistedt and Jason McEwen finished developing the first exact harmonic and wavelet transforms in 3D spherical coordinates. The paper has now been peer-reviewed and will be published in IEEE Trans. Sig. Proc. in December. The code is available on www.flaglets.org.
Why exact? Exact transforms are essential in information sciences because they enable one to capture all the information contained in a complex signal, and process it without any loss of information. Thanks to this theoretical property, the accuracy achieved by the transform is only limited by the representation of floating-point numbers on the computer!
Why wavelets? Wavelet transforms are increasingly successful in various disciplines (including astrophysics and geophysics) because they separate scale-dependent, localised features in the signals of interest, which is very suited to the extraction of patterns in complex data. As an example they were used by Stephen Feeney and Hiranya Peiris to search for potential signatures of topological defects in the cosmic microwave background.
Why in three dimensions? In astrophysics, spherical wavelets are naturally suited to the analysis of signals on the sky, and cosmologists have already started to apply them to galaxy surveys, for instance to help dealing with the systematics or to isolate structures at different physical scales of interest. However galaxy surveys are 3D datasets where the angular position is accurately measured on the sky but the radial information (such as photometric redshift or distance) is often estimated from color information and therefore subject to uncertainty. Not only one should use 3D wavelets to properly treat such data, but these wavelets should furthermore separate the radial and angular features to avoid mixing of radial and tangential systematic uncertainties. The accuracy would also be critical because most modern pipelines apply these transforms repeatedly (to go back and forth from pixel to wavelet space), leading to a loss of information if the transform is not exact.
3D sampling theorem for the Fourier-Laguerre transform
What is the outcome? To address these problems, Boris and Jason designed a 3D harmonic transform combined with a sampling theorem on the ball, namely a 3D pixelization scheme that captures all the harmonic information in a finite set of samples on the ball. Then, they defined wavelet kernels, called “flaglets”, to extract scale-dependent, localised features in signals defined on the ball. The flaglets isolate patterns in the radial and angular dimensions separately and are very promising for analysing galaxy surveys and treating their systematics.
The code is fast, accurate, and is publicly available on www.flaglets.org.
Flaglet transform of a N-body simulation. The top left signal is the input data, and the following signals are the flaglets. Click on the image to see larger version.
