Written by visiting collaborator and guest blogger Matt Johnson.
Computer simulations of the early universe allow us to explore scenarios that are just not possible to examine using pencil-and-paper calculations. I was recently in London working on how to use computer simulations to predict the observable signatures of eternal inflation. In the standard story of eternal inflation, our universe is purported to be enclosed inside one bubble among many, each expanding into an inflating background space-time. Our bubble undergoes collisions with others, providing a possible observational window on this bizarre scenario (read about the latest tests in this paper).
The field configuration making up our bubble determines the properties of our cosmology. For example, the symmetry of a single bubble fixes the universe to be an open Friedmann-Robertson-Walker (FRW) space-time. However, the collision between bubbles upsets this symmetry, meaning that if we live inside a bubble which underwent collisions, there will be deviations from a purely open FRW space-time.
The equations governing the evolution of the fields making up the bubbles and gravity are highly non-linear, making computer simulations a necessary tool for finding the exact space-time resulting from the collision between bubbles. Setting our sights on understanding the collision between pairs of bubbles, there is enough symmetry to evolve in 1 space and 1 time dimension. Last year, we wrote a code to simulate the collision between two bubble universes (you can read about our first results in this paper). One shortcoming of this original work was that the coordinates we used prevented us from evolving for longer than a few e-folds of inflation. We’ve fixed that by introducing a more appropriate set of coordinates, and now the challenge is to extract the cosmology contained inside one of the bubbles.
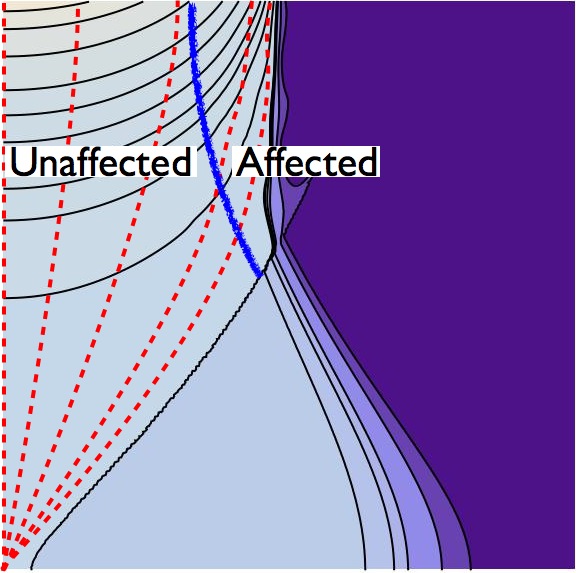
For colliding bubbles, one no longer has a purely homogeneous and isotropic cosmology. However, if collisions are to be consistent with what we observe, there had better be regions where the space-time is approximately FRW. So, how does one identify which regions are approximately FRW from the simulation data? How does one then quantify the deviation from FRW, so that quantitative predictions can be made? Our current method tracks the behaviour of geodesics evolved through the simulation. Because we know how geodesics would evolve through a purely FRW universe, we can determine the qualitative and quantitative differences. This is depicted schematically in the figure below, where I’ve shown the results of a simulation, and some of the geodesics evolving in the background. The geodesics entering the affected region pile up, indicating a deviation from pure FRW. We hope to polish the final code off soon, and extract the first observational signatures from our simulations!