Quantum Bubble Collisions

On 25 June, 2015, in Outreach, Papers, People, Science, by admin

This post was written by Jonathan Braden.

NOVA’s The Nature of Reality recently dedicated a blog post to my work on bubble collisions with J. Richard Bond and Laura Mersini-Houghton. The post focussed on one possible observational consequence of our findings. Here I’ll outline a little more precisely what we did in our work. For more information see my webpage.

Inflation, Bubble Universes and the Multiverse

Modern cosmology posits that the very early universe underwent a period of rapid expansion known as inflation. Inflation smoothes out the cosmos, creating the large-scale homogeneity we observe today, while simultaneously leaving small wrinkles that eventually form structures such as galaxies. However, it turns out that once inflation begins it may continue forever. In this ‘eternal inflation’, an omniscient being able to view the entirety of the universe at once would see vast swathes of space continuing to inflate. Only in special pockets has inflation ended, allowing structures such as galaxies to form and life as we know it to exist. This large collection of “pocket universes” is one incarnation of the multiverse.

Two mechanisms may cause eternal inflation, both of which can be visualized by thinking about a ball rolling down a mountain. The multiverse can be pictured as many copies of this mountain, each located at a different point in space and each with its own ball. New space is created in regions that are inflating, so the mountains in these regions replicate to fill the rapidly expanding space. The rate at which space is being created, or how quickly a given mountain replicates, is determined by the height of the ball above sea level. When a ball approaches the bottom of a mountain, inflation ends in that region. The mountains aren’t completely smooth: there are many ridges, long valleys and depressions along the way, which affect the ball’s trajectory and determine how long it takes to reach the base. There are also regular wind gusts that get stronger as we climb higher up the mountain. The mountaintop is extremely windy, while the base is calm. The wind represents the effects of quantum mechanics on the rolling balls and is produced by inflation. The strength and direction of the gusts varies from mountain to mountain. However, each individual gust affects a large spatial volume and thus pushes the balls on several different mountains at the same time.

In one type of eternal inflation, which I’ll call stochastic eternal inflation, the wind is so strong that it can push the ball back up the mountain. Balls that move up the mountain then replicate, so that there are always some balls that remain trapped near the top of the mountain, i.e. some regions of space are always inflating.

In the second type of eternal inflation, called false vacuum eternal inflation, the ball instead rolls into a depression and gets stuck. Without quantum mechanics, this would be the end of the story and the ball would sit there forever. However, the ball may escape in two different ways. In one case, the wind is strong enough to blow the ball out of the depression and it once again starts rolling down the hill. In the other case, the depression is so deep that the wind can’t extract the ball from it. However, there is another quantum mechanical effect. As an (imperfect) analogy, suppose that thunderstorms occasionally pass over the mountain and the rain fills the depression so that it forms a pond. Eventually the pond overflows and the ball escapes with the water to once again start rolling down the mountain. In physics lingo, the region has quantum mechanically tunnelled out of the depression. The thunderstorms are more localised than the wind gusts, so the regions that tunnel are smaller than the regions blown around by the wind. In the actual universe these tunnelling events correspond to the creation of new bubble universes.

In this final scenario, the universe on very large scales looks like a pot of boiling water, with a universe like our own existing within each of the bubbles of steam. The water in this case has the strange property that it is continually expanding and replenishing itself, so that the pot of water gets larger and larger. As a result, new water is constantly becoming available to nucleate new bubbles. Once in a while two bubbles will nucleate close enough to each other that they run into each other as they expand. From our viewpoint living within one of the steam bubbles, it looks as though our universe has collided with another universe.

Symmetric Collisions

Previously, physicists have always assumed that if we were to videotape a collision between two bubbles, then the video would look exactly the same if we spun the video camera around in certain ways or if we jumped in a car and drove away from the two bubbles at a constant speed in certain directions. To use a physicist’s favourite word, the collision is said to possess a large amount of symmetry. The symmetry is really a combination of two different types of symmetries: a rotational piece and two boost pieces. These correspond to rotating our video camera and driving away in a car, respectively. To visualize the rotational part, first imagine that each bubble is a perfectly spherical ball. In a collision we have two balls, so imagine connecting the two bubbles by a thin string to make a barbell. After nucleating, each bubble expands so the length of the string decreases with time until eventually the bubbles collide. Now, if you grab one ball in each hand and rotate the whole thing around this string, the collision will look exactly the same. The boost symmetry is a little bit stranger, but basically if you took one ball in each hand and threw them away from you at the same speed and with their centres parallel to each other, then the resulting collision will be the same regardless of how fast you throw the two balls.

When we make these symmetry assumptions, then we often get collisions that look like the figure below. To visualize what’s going on, think of each bubble as a rubber ball that is being inflated while its center is held fixed. As they are inflated, each ball gets bigger and bigger, just like a balloon. Eventually the balls become large enough that they hit each other. When the rubber walls of the balls collide, they bounce off of each other, making a dent. These dents then spring back out and bounce off each other again, and the whole process repeats. A video illustrating this can be seen in the YouTube link below.

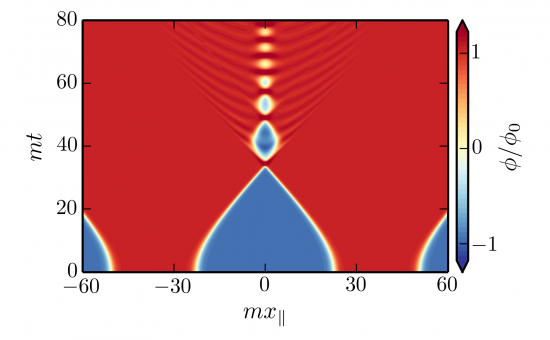
Figure 1: Collision between two bubbles assuming the rotation and boost symmetries described in the main text. The horizontal axis measures position along the barbell string (see analogy in the text above) and the vertical axis measures time since nucleation of the bubbles. Red is inside the bubbles, blue is outside the bubbles, and white shows the location of the bubble walls.

Collisions with Quantum Mechanics

However, the situation described above isn’t the full story. Thanks to quantum mechanics, there is inevitably some jitter around the perfect spheres. To use the same analogy I gave in the article, imagine that each bubble is a globe with small bumps and ripples from the various land masses, mountains, and valleys. If we spin the globe around, the positions of the continents, oceans, and mountain ranges change so that it no longer looks identical when viewed from different directions. Once again using a physicist’s language, we say the symmetry has been broken.

As I mentioned, these mountain ranges and valleys must be present, or else we would be violating the laws of quantum mechanics. However, they also serve two much more practical purposes in the inflationary multiverse: the bubbles nucleate because of the quantum jitter, and the quantum fluctuations eventually form all of the galaxies and other structure that we see in the universe around us. Therefore, the entire picture of our observable universe living within a bubble nucleated in a much larger multiverse relies heavily on this quantum jitter.

In our series of papers (here, here and here) we studied the effects of this quantum jitter on bubble collisions. When the bubbles first nucleate, the fluctuations are small and you would have to look very carefully to see that the bubbles are not perfect spheres. Again viewing each bubble as a globe, you would need to pull out a magnifying glass in order to see that there are small mountains on the surface. However, it turns out that the collisions of the bubbles can make the jitter grow very fast. In the figure below, I’ve illustrated the difference between having no quantum jitter (left panel) and small initial fluctuations (right panel). The collision with the initial jitter is seen in the YouTube video below. The mountains (valleys) on the parts of the globes that dent in and out during the collision quickly grow in height (depth). In other words, mountain ranges grow on the parts of the walls that continually bounce off of each other. The first few times the bubble walls bounce off of each other, the mountains are still small so things look basically the same as if the bubbles were perfect spheres. However, it doesn’t take long for the mountains to get very high (much higher than Mount Everest). In the next collision, rather than the walls of the balls bouncing off of each other, the mountains instead poke holes in the bouncing walls. The walls quickly dissolve, leaving behind some small remnants in the collision region.

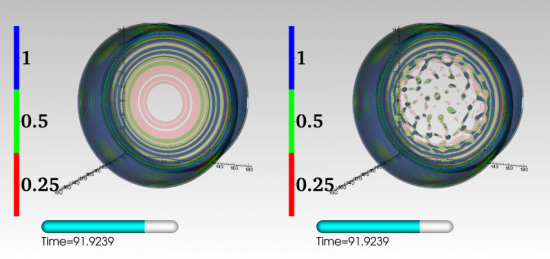
Figure 2: Here we show the distribution of energy for both a collision with no quantum jitter (left) and a collision with quantum jitter (right) at a point after the initial quantum fluctuations have become very large as a result of the collision. Quantum mechanics dramatically changes the final outcome of the collision.

New Phenomenology and Future Work

As seen in the figures and videos above, including quantum fluctuations can significantly alter the outcome of bubble collisions. This forces us to re-evaluate our current understanding of bubble collisions in the multiverse. Two of the more exciting possibilities are the production of gravitational waves during the pairwise collisions of bubbles, and the creation of black holes from the collisions. In the treatment based on rotational and boost symmetries, both of these effects are ignored because the symmetry assumptions forbid them from occurring. The former of these effects was emphasized in the NOVA post on our work, and it could provide a new observational signature from bubble collisions in the multiverse. This is very exciting, since this could give us an additional observational handle with which to test the multiverse.

Acknowledgments

A big thank-you to Belle Helen Burgess and Hiranya Peiris for editing and comments.

You can read more here:

NOVA blog post
Gravitational Waves from Bubble Universe Collisions?