This guest blog post was written by Aurélien Benoit-Lévy.
The cosmic microwave background (CMB) is the furthest light we can observe. Since it is the furthest, bright galaxies and other compact objects can pollute in a nasty way the superb observations of the CMB that forthcoming experiments will soon deliver. To get rid of these point sources, we need to mask them. This is of course not harmless, as the resulting map is punched with holes just like emmental!
Holes in a map are unfortunate as they considerably complicate the spectral properties of the signal under consideration. But if there is a problem somewhere, it means that there is a solution, and I’m sure you would have guessed the solution: inpainting! Inpainting is just like cod, it’s good when it’s well made. The basic idea is to fill the holes with some fake data that would mimic some properties of the original signal. There are plenty of methods to inpaint a hole. For instance, the simplest one would be to fill the hole with the mean of all the surrounding pixels, but we can do much better than that.
CMB has a nice property: it’s correlated. This means that the probability that a given pixel has a given value is not independent of the value of the other pixels. And the CMB is also (very very close to) Gaussian, so we can use those two properties to generate random constrained Gaussian realizations that mimic the lost signal, but preserve the statistical structure of the map. Basically, we can use the information contained in the non-contaminated region to guess the most probable value in the holes. This technique has been known for quite a while, but sometimes requires heavy computations to accurately take into account all the information available in the map.
In recent work, my collaborators and I have demonstrated that it is not necessary to account for the whole map to inpaint a small hole. Using only the neighboring pixels is enough. With this method, we are able to inpaint a realistic CMB map, with a realistic point source mask in a realistic time! And the statistical properties of the inpainted maps are virtually unchanged! We applied this locally-constrained Gaussian realization in the special case of CMB lensing reconstruction and showed that this tool is very efficient, as it preserves the two-point statistic, and – above all – does not generate a spurious four-point signal. Of course, I now need to tell you about CMB lensing and four-point statistics, which is a very big thing and we’ll hear a lot about it in the coming months. But that will be for another post!
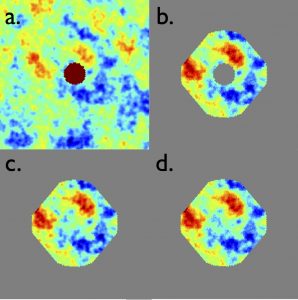
(a) CMB map with a point source hole, (b) neighbouring pixels used to inpaint the hole, (c) Input map, (d) Inpainted map
You can read more here:
Aurélien Benoit-Lévy et al.
Full-sky CMB lensing reconstruction in the presence of sky-cuts.
